Marr's Levels are Not Dead

Marr's levels are Aristotelian causes and are not dead.

MIT Neuroscientist David Marr died of leukemia in 1980 at the age of 35. Two years following his death, his book Vision was published and forever entered the cognitive science canon. While most students of cognitive science won’t be able to tell you much about Vision or what Marr’s actual research program was about, all of them will be able to tell you about the implementational, algorithmic, and computational levels. Since the publication of Vision, Marr’s three levels have been a cornerstone of cognitive science writ large. It’s generally from Marr that terms like equifinality, functional equivalence, isomorphism, and weak equivalence are invoked in cognitive science, allowing us the ability to describe systems as different from one another as brains and computers as performing the same or similar functions.

Despite the popularity of Marr’s framework, much confusion about these levels remain. More recently, the relevance of this framework to information-processing systems has been brought into question with large-scale neural network inspired algorithms which perform diverse computations using the same underlying architecture. During my work at UCLA’s Institute for Pure and Applied Mathematics long program on The Mathematics of Intelligences this semester, I conducted a deeper dive on Marr and his framework and think I’ve come up with an easier way of explaining it. Namely, I think that Marr’s framework is virtually the same as Aristotlean causality and, for the purposes of teaching, can be most easily described in those terms.

Explaining the levels at IPAM’s Lake Arrowhead retreat

Marr’s Levels

Marr’s levels appear in Chapter 1 of Vision, although they precede the publication of the book by six years in a publication with Tomaso Poggio titled, “From understanding computation to understanding neural circuitry.” In the book, Marr proposes three levels for understanding any information processing system (e.g. a portion of the brain, the brain itself, or a computer). These levels are:

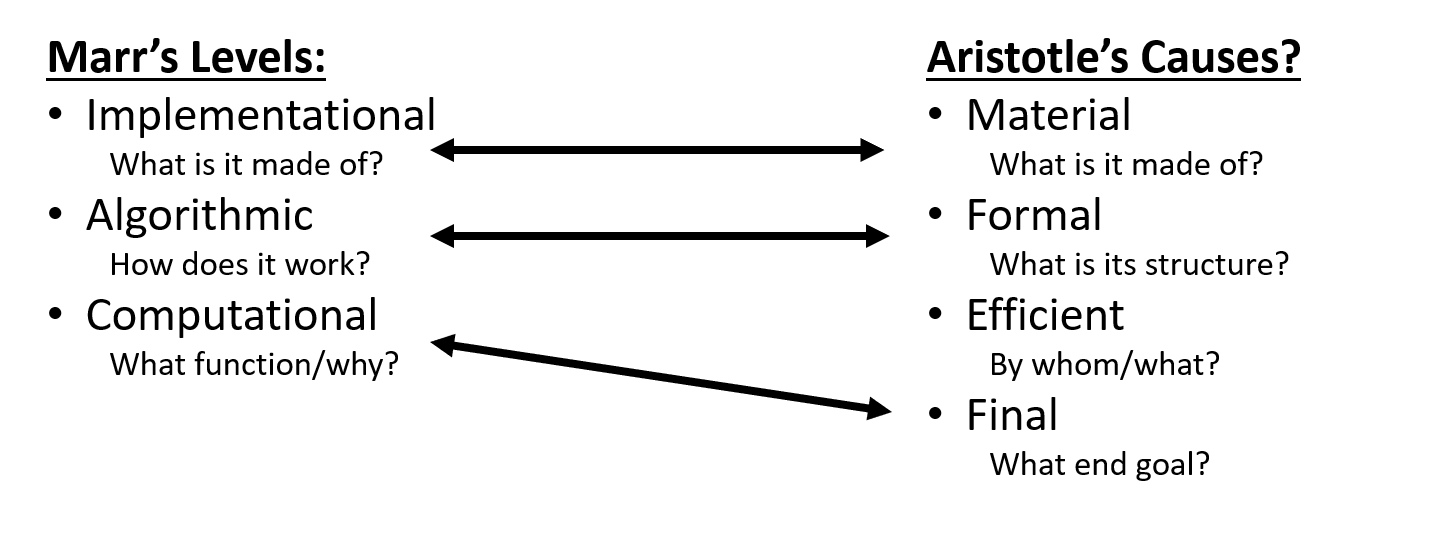
• Implementation: What is the hardware of the system implementing the information processing? Are we speaking of neurons or silicon chips?

• Algorithm: How does information processing take place? Specifically, what are the inputs and outputs of the system? What processual rules does it use to transform these inputs into outputs?

• Computation: What is the goal of the information processing system? You hear this level described both by Marr and others as the “what and why.” It more specifically refers to “what function” and “why”.

  

  From Vision (1982)

In addition to these three levels, in the original article, Marr and Poggio describe a fourth one between implementation and algorithm, which I would describe as the Rules level, which basically lists the affordances of an information-processing system’s implementational hardware: can an ANN solve an XOR problem, does it add/subtract, does it have to do something else? And so on. This level was dropped in Vision and is usually not discussed.

The point of Marr’s three levels are to give you three ways of describing any given information processing system. Without appealing to implementation, you may be able to ask how it is that brains and computers are doing the same things, what sort of information processing is emergent or partially sealed off from its lower levels. The problem is that Marr is generally confused: these processes are usually described as top-down, even by Marr himself, rather than bottom-up, and even sufficient researches have assumed that even Marr’s levels require a commitment to a computational level to exist for every information processing system. This has led to a great deal of confusion. Many also find the Computational - Algorithmic distinction unclear.

Aristotelian Causality

I have had trouble teaching this concept. The last time I TA’d Introduction to Cognitive Science, I was amazed at how each of the five TAs had completely different views of what these levels were. But actually what Marr is describing here is a quite old line of reasoning, and one which was present in Aristotle’s Four Causes. I am not sure if Marr intended his levels to reflect Aristotlean causality, as Aristotle is never referenced in relation to it (although he is referenced in Vision, in the book’s first sentence), but the mapping is basically one-to-one.

In Metaphysics, Aristotle argues that there are four types of answers to a “why” questions for any given process or object. These four types are called Causes, although do not relate to causality in a Newtonian sense. You should think of Cause in this case instead as “description” or “explanation”. These causes are:

• Material: What is it made of?

• Formal: What is its structure and how does that structure make it that thing?

• Efficient (Agential): By whom/what was it brought about? (This is closest to our modern notion of “cause”)

• Final: Why does it exist? What is its teleology?

Take a barn, for example. Its material cause includes the wood and nails which constitute its structure. Its formal cause is the plan of the barn, its overall structure which makes it a barn and not a pile of wood and nails. Its efficient cause refers to the builders, the tools, and the machinery and the process of construction. Its final cause, or its purpose, is the reason it exists, which is to provide shelter to animals.

Although all of these causes, except for Efficient causality, for describing something have fallen out of favor for describing things in scientific parlance, this schema was important to us prior to the age of Newton. Notably, in the 13th Century, Thomas Aquinas turned this into a top-down schema wherein the material cause supervenes on the formal cause which supervenes on the efficient cause which supervenes on the final cause, giving us some grist for the eventual mill of “emergence”. In more recent decades, bi-directional feedback between these, in particular between the formal and efficient cause, have given us more modern notions of “circular causality” (Witherington, 2011) in the philosophy of complex systems. I thus find this framework pretty useful in my own work as a cognitive scientist.

We can see how Marr’s levels and Aristotle’s causes map to one another almost perfectly below. The implementational level is straightforwardly material cause. The algorithmic level, what form the information processing system takes that makes it an information processing system maps to the formal cause. The computational level is precisely final cause.

One mapping is missing between efficient cause and Marr’s levels. While Marr did not have a level for this, oddly enough, in 2012 Poggio published an article titled “The Levels of Understanding Framework, Revised.” In it, he argues, “and I am sure that David would agree — that learning should be added to the list of levels of understanding, above the computational level.” He actually adds two separate levels: learning and evolution, as more or less the same process across different timescales. Adding Poggio’s revision, without intending to make this framework map directly to Aristotle, we get a full mapping of information-processing systems like this:

Final Cause and Theories of Artificial Intelligence

Coming back to something referenced earlier in this post, a debate which has been present in cognitive and computer science is whether Marr’s levels are effectively dead. This is thought to be the case because modern artificial intelligence, through the use of extremely complex algorithms, have come to be applied to a diverse number of problems, effectively rendering the computational level, and Marr’s own top-down framework, useless.

Now, I guess this could be true if at any point you forced yourself into a naive, colloquial view of what these levels are supposed to be about and demanded that a computational level must exist for each type of system (not to mention that Marr’s original framework was designed specifically for describing biological and biology-inspired systems - but let’s grant it’s more general than this for the reason that it is). The problem is that the computational level has the same problem that Aristotle’s final cause does, which is that it is not apparent whether or not a process you are looking at exhibits a telos, or end-directed goal, in general. Some things do and some things do not. When looking at atoms colliding out in the universe, it is not apparent that these are guided towards an end-goal. But when examining the unfolding of an embryo into a fully-fledged organism, it is irrefutably the case that the embryo’s algorithmic instructions have given it an end-directed goal or form to move towards.

Marr was not ignorant of this challenge. In one of the last papers published before he died, titled “Artificial intelligence — a personal view,” Marr builds upon his Levels framework to address this specific problem. In the essay, Marr argues that at least two separate theories, with theories being used to refer to forms, constructions, or instantiations (I will call them systems), exist for building new information-processing systems and describing those in the real world.

In this new framework, Type I systems are those which clearly exhibit a computational level, or a telos, and have an end-goal in mind. In fact, some elaborations of Type I systems (such as Chomsky’s universal grammar theories) almost entirely disregard the algorithmic or implementation details. And often times, for a Type I theory, the computational process is known but the algorithmic is not. Marr goes on to state, “while many problems of biological information processing has a Type I theory, there is no reason why they should all have.”

Systems lacking computational, or Type I theories, are referred to as Type II theories. In this framework, Type II theories are those in which their own interaction or their own algorithmic level is the best description. In the modern artificial intelligence ecosystem, this is what the transformer architecture is. It’s a complex systems which performs a large number of information processing and it is best described in terms of its architecture rather than in terms of its end-directed “computation”. They do not exhibit a computational level and do not need to be described on that level.

The “principal difficulty” Marr states, for AI research, is trying to figure out when you are in Type I or Type II space. While many systems and problems have Type II solutions, they may also have a Type I theory: again, identifying final cause or computation is difficult because the telos of a thing is not in the thing itself - it is, as Terrence Deacon would put it, an absential feature. The danger here is that when we are in Type II space where an undiscovered Type I theory exists, it means that a simpler algorithm to the problem can be designed, we just simply don’t actually know how our system works. On the other hand, Type I hallucinations often occur in Type II space: we come up with representational views of what non-representational systems are doing and attempt to generalize from there. Both of these are major issues we see in AI research today, telling me that not only Marr’s levels, but Marr’s Type I/Type II distinction still have a relevance to our research today and that conceptually things are messier than ever.

Finally, one aspect of Marr which was not ever fully explored in his lifetime, is that of emergence and constraints: as I reference before, while Thomas Aquinas and Marr himself partially thought that their frameworks were top-down, the bottom-up component cannot be ignored. In particular, the implementation level seems to be the most silent of the levels and linking implementation to algorithm, or perhaps more critically, linking implementation to computation and skipping algorithm altogether should be explored (again, read my blogpost on Terrence Deacon). Linking learning and evolution to any of these processes and developing a notion of information-processing systems designing algorithms, of discovering how computational levels emerge in the history of life, of understanding multi-scaled systems in this framework, are not just open questions in computation and biology, but active research programs where there is a lot more work to be done. Marr’s levels are not dead, but perhaps the more colloquial notion of the framework is and should be so that we can move on from mere categorizing to actually theorizing.

References and Additional Reading

Brase, G. L. (2014). Behavioral science integration: A practical framework of multi-level converging evidence for behavioral science theories. New Ideas in Psychology, 33, 8-20.

Insel, Nathan, and Paul W. Frankland. "Mechanism, function, and computation in neural systems." Behavioural processes 117 (2015): 4-11.

Marr, D. (1977). Artificial intelligence—a personal view. Artificial Intelligence, 9(1), 37-48.

Marr, D., & Poggio, T. (1976). From understanding computation to understanding neural circuitry.

Marr, D. (1982). Vision: A computational investigation into the human representation and processing of visual information. W.H. Freeman.

Poggio, T. (2012). The levels of understanding framework, revised. Perception, 41(9), 1017-1023.

Witherington, D. C. (2011). Taking emergence seriously: The centrality of circular causality for dynamic systems approaches to development. Human Development, 54(2), 66-92.